はじめに
こんにちは。キャディで原価計算システムの開発を担当しております、高橋です。 この記事は キャディ Advent Calendar 2020 の23日目です。前日は朱さんの 「【開発カルチャー発信 vol.1】原価計算システム開発チームの開発理念を大公開!」でした!
さて本日は掲題の通り、私がスキルアップを兼ねて趣味的に取り組んでいる、コストモデル可視化システムの開発について紹介させていただきます。
目次
[toc]
課題意識
弊社のビジネスの核は、コストモデル
コストモデルは、名前の通り「コスト」の計算を「モデル」化したことで、原価計算という作業を弊社内で民主化しました。「正しい原価」を誰でもすばやく計算できるということです。
これが無くては弊社のビジネスがスケールアウトすることは不可能であり、スケールアウトしなければ受発注プラットフォームは作れません。従って、弊社のビジネスの核は1にも2にもコストモデルなのです。
コストモデルは生き物
しかしこの「正しい原価」というのが曲者です。正しいの定義は時々刻々と変わります。従って、コストモデルはこの正しさに常に追従する必要があります。
例えば材料費が高騰したら、原価は変わります。また、弊社が今まで対応していなかった新しい加工方法をコストモデルで取り扱えるように拡張しないと正しい原価が出せない場合もあります。このような事情で、コストモデルは常に改訂・拡張を繰り返しながら、あるべき原価を求めてさまよい続けています。
しかし、コストモデルは見えにくい
このように、弊社ビジネスの核でありながらも常に動き続けるコストモデルですが、現状はRustのソースコードで実装されています。従って、コストモデルを常日頃からメンテナンスしている立場でない限り、具体的にコストモデルの定義がどうなっているのか把握しにくいというデメリットがあります。
コストモデルを作るのではなく扱う立場であっても、コストモデルが前提とするコストの構造・概念を理解していることは重要なのですが、ここで「コストモデルが見えにくい」ということが障壁になっていると私は考えています。
コストモデルをどうやって可視化するか
可視化したいものがコードの中にしか無い
上記の通り、現状ではコストモデルの定義はRustでハードコーディングされています。 こんな感じのものがたくさんコーディングされています。
コストモデルの定義の例(体積計算):
原価 = 加工時間 × 時間当たり原価
加工時間 = 加工工程 XXX の時間 + 加工工程 YYY の時間
時間辺り原価 = とある定数
加工工程 XXX の時間 = XXX加工単体の時間 × XXX加工の数
加工工程 YYY の時間 = XXX加工単体の時間 × XXX加工の数の2倍
抽象的に書いていますが、例えば穴あけ加工が1個1分かかってそれが2箇所、1分あたり100円なら、概算で200円、みたいなことを考えるとわかると思います(実際にはこんな単純ではなく、もっと複雑です)。
ここから可視化しようと思うと、Rustのコードをパースしてコストモデルの定義を抽出してくるような仕組みが必要ですが、あまり現実的ではありません。
コストモデルの定義をデータとして分離する
コストモデルは数式のグラフ
上記の例から分かるように、コストモデルは数式の集合であり、それらは依存関係を持つことから、数式や定数(引数を持たない数式)をノードとする非循環有向グラフ(DAG)を考えることができます。これを数式グラフと呼ぶことにしましょう。
上記の定義を数式グラフとして表現した例:
例えば上図のように表現された数式グラフを計算する場合は、依存の階層の一番下から順番に計算していくと、最終的に原価を求めることができます。コストモデルの定義がどのようなものであれ、計算可能な関数と依存関係の集合であれば可能なことです。
グラフ構造をデータとして計算処理から分離できる
さてこのように考えていくと、コストモデルの定義は数式グラフの中にしか登場せず、数式グラフの計算処理には登場しません。したがって、現状のようにプログラム中にコストモデルの定義をハードコーディングせずに、どこかにデータとして保存された数式グラフを計算実行処理に外側から注入して結果を得る、というやり方ができそうです。要は、コストモデルの定義を数式のグラフ構造のデータとして、計算処理から切り離すということです。
このやり方であれば、グラフ構造の保存・編集・可視化ができれば、コストモデルを可視化できると言えそうです。Rustのプログラムをパースしてコストモデルの定義を解析するよりも、大分現実味があります。
技術選定とシステム構成
上記のやり方を試すために、Frontend, backend, db を直列につないだ極めてシンプルな構成でシステムを組んでみることにしました。
| component | 仕様技術、ライブラリなど | 役割 |
|---|---|---|
| Frontend | React + Typescript , G6.js, typed-rest-client | 数式グラフと計算結果の表示 |
| Backend | Java + Spring boot + Spring Data Neo4j, mxParser | 数式グラフのロードと計算 |
| DB | Neo4j | 数式グラフの保存 |
まず、数式グラフを保存する手立てとして、グラフ構造をそのまま扱えるグラフ指向データベースを使うことにしました。とりあえず今回は、一番有名っぽいNeo4jにしました。
すると、Neo4jとエンティティ定義のマッパー(ObjectGraphMapping)に対応したフレームワークであるSpring Data Neo4j を使うのが一番楽につくれそうなので、バックエンドはJavaに決定。
バックエンドでは数式グラフを計算するので、Neo4jに文字列として保存された数式(簡単のために算術演算に限定)を動的にパースして計算する処理が必要になるのですが、そのようなライブラリをJavaから探した結果、mxParserというのがあるので使ってみました。「キャディのエンジニアなんだからパーサーくらい自分で書け」と言われそうですが、今はサクサク作って動かしたいので、あるものは最大限活用します。
UIは、業務上のスキルアップも兼ねてReact + Typescript を使うことにしました。グラフ構造を描画するUIライブラリとしては、G6.js を使ってみました。弊社で使用実績はなさそうなものの、MITライセンス・機能が豊富・公式ドキュメントが充実の3点で決めました。バックエンドのAPIを叩くクライアントは、本家が作ってて信頼できそうなのでtyped-rest-clientに(適当)。
実装
今回は簡単のため、UIからのコストモデルへのパラメータの入力は受け付けないものとします。 また、コストモデルの編集は実装が多いので、ここでは割愛します。 データベースに予め数式の定義と入力が保存されている状況から、計算と表示ができるところまでを紹介します。 特に難しいことはしていないので、同じものはこの記事を読みながらどなたでも作れると思います。
Backend
ここでは、この記事のために「数式グラフのロード」「数式グラフの計算」の2つのAPIを用意してみます。
Entity定義
ノードに数式をもたせて、ノード間のエッジに、数式同士の依存関係と、依存先の数式が対応する依存元の数式中の変数名を保持させます。 SpringDataNeo4j のおかげで、クラスにアノテーションを付けるだけでグラフの構成要素として設定できます。
@NodeEntity
public class ExprNode {
@Id
@GeneratedValue
public Long id;
public String name;
public String expr;
@Relationship(type = "SUBEXPR", direction = Relationship.OUTGOING)
public ArrayList<Edge> subExpressions = new ArrayList<>();
// 依存先の数式を定義する関数
// 第二引数で、数式中のどの変数に第一引数の数式の評価結果を割り当てるかを
// 指定している
public boolean setSubexpr(ExprNode node, String token) {
Expression expr = new Expression(this.expr);
this.subExpressions.add(new Edge(this, node, token));
}
// 自身の値を計算する関数。
// 関数の引数の値が別の関数で求まる場合、再帰的に潜っていって計算する。
// Expression は mxParser が提供する数式型。
public Double evaluate() {
// ここで文字列の数式をパースして関数を生成すると同時に、関数の引数に依存先の関数の評価結果を割り当てる
Expression expression = new Expression(this.expr, this.subExpressions.stream()
.map(edge -> new Argument(edge.startToken, edge.end.evaluate())).toArray(Argument[]::new));
return expression.calculate();
}
}
@RelationshipEntity(type = "SUBEXPR")
public class Edge {
@Id
@GeneratedValue
public Long id;
@StartNode
public ExprNode start;
@EndNode
public ExprNode end;
// startnode の数式のどの 変数名に endnodeが対応するかを保存するフィールド
public String startToken;
}
Repository
Neo4jにアクセスするインターフェースを定義し、数式グラフをロードしてくる関数を定義します。 これもSpring DataNeo4jの恩恵を受けることが出来て、interface さえ定義すれば実装はSpringが勝手に作ってくれます。
public interface ExpressionRepository extends Neo4jRepository<ExprNode, Long> {
// cyper query を直接書くこともできる
@Query("MATCH p=(n:ExprNode)-[:SUBEXPR *]->(:ExprNode) RETURN nodes(p), relationships(p)")
ArrayList<ExprNode> getAllExprNodesWithEdges();
// query を書かない場合、実装は関数名から自動で定義される
// デフォルトではグラフの深さ1までしか取ってきてくれないので、アノテーションで指定する
@Depth(value=4)
Option<ExprNode> findByName(String name);
}
Service
作りたいAPIには、DBへの数式グラフのシード、数式グラフの取得、数式グラフ計算の3つの処理が必要なので、それをここで用意します。
@Service
@Transactional
@EnableNeo4jRepositories(basePackageClasses=ExpressionRepository.class)
public class ExpressionService{
@Autowired
ExpressionRepository expressionRepository;
// 数式全体の取得
// 戻り値は適当に用意したResponse型
public ExpressionsResponse getAllExpressions() {
ArrayList<ExprNode> nodes = expressionRepository.getAllExprNodesWithEdges();
ArrayList<NodeResponse> nodeResponses = nodes
.stream()
.map(node -> {
return new NodeResponse(node.id, node.name, node.expr);
}).collect(Collectors.toCollection(ArrayList::new));
ArrayList<EdgeResponse> edgeResponses = nodes
.stream()
.flatMap(node -> {
return node
.subExpressions
.stream()
.map(edge->{
return new EdgeResponse(edge.id, edge.start.id, edge.end.id, edge.startToken);
});
}).collect(Collectors.toCollection(ArrayList::new));
return new ExpressionsResponse(nodeResponses, edgeResponses);
}
// 架空の体積計算を表す数式グラフを保存してみる
public String seedExpressions() {
// 数式ノード定義
ExprNode volume = new ExprNode("volume", "x * y * z");
ExprNode x = new ExprNode("x", "10");
ExprNode y = new ExprNode("y", "10");
ExprNode z = new ExprNode("z", "a + b");
ExprNode a = new ExprNode("a", "20"); // 定数
ExprNode b = new ExprNode("b", "30"); // 定数
// 数式中の変数に別の数式を割り当てる。
volume.setSubexpr(x, "x");
volume.setSubexpr(y, "y");
volume.setSubexpr(z, "z");
z.setSubexpr(a, "a");
z.setSubexpr(b, "b");
expressionRepository.save(volume);
return volume.name;
}
// 数式グラフ中の指定した数式ノードの値を計算する
public double calculateExpression(String name){
ExprNode rootNode = expressionRepository
.findByName(name)
.orElseThrow(() -> new RuntimeException());
return rootNode.evaluate();
}
}
Controller
RestAPI経由でそれぞれのビジネスロジックを呼んでResponseを返すようにします。
@RestController
@RequestMapping("/")
// UI は yarn start で立てるので、そのアドレスをcorsに設定
@CrossOrigin(origins = "http://localhost:3000")
@ResponseBody
public class Controller {
@Autowired
ExpressionService expressionService;
// 数式グラフをシードしてロード
@RequestMapping(value = "/expressions", method = RequestMethod.GET)
public ExpressionsResponse readExpressions(@PathVariable String version) {
expressionService.seedExpressions(version);
return expressionService.getAllExpressions(version);
}
// 数式グラフの計算
@RequestMapping(value = "/calculate", method = RequestMethod.GET)
public String calculateSeededNode(@PathVariable String version) {
// DB初期化
String rootNodeName = expressionService.seedExpressions(version);
return String.format("calclation finished: %f", expressionService.calculateExpression(rootNodeName, version));
}
};
UI
こんな感じで、Reactのコンポーネント内でG6.jsのグラフオブジェクトを初期化した後、バックエンドからグラフ取得したグラフのデータを流し込んで描画します。(長いので一部省略しています) G6.js は pureJS ライブラリなので、Reactに組み込むのがちょっと手間です。公式のサンプルを元に実装しましたが、そのままだと警告が出るので一部手を加えました。
function GraphView() {
const ref = React.useRef(null);
const graph = React.useRef<Graph | null>(null);
useEffect(() => {
if (!graph.current) {
graph.current = new G6.Graph({
container: ReactDOM.findDOMNode(ref.current) as HTMLElement,
layout: {
type: 'dagre', // 有向グラフを階層的にレイアウトするためのアルゴリズム
rankdir: 'LR', // レイアウトの向きを指定
ranksep: 70, // レイアウト方向のノード間隔を指定
},
// グラフ上で描画されるノードのデフォルト設定
defaultNode: {
type: 'modelRect',
anchorPoints: [
[0, 0.5], // source
[1, 0.5], // target
],
// ...その他設定は省略
},
// グラフ上で描画されるエッジのデフォルト設定
defaultEdge: {
// ノードのアンカーポイントのどれとどれをつなぐかを
// defaultNode の anchorPointsのindex指定で設定
sourceAnchor: 1,
targetAnchor: 0,
},
});
}
let rest: trc.RestClient = new trc.RestClient('test', 'http://localhost:8080/');
rest
.get<ExpressionsResponse>(`expressions`)
.then((res: trc.IRestResponse<ExpressionsResponse>) => {
let data: GraphData = {
nodes: res.result!.nodes.map(/* G6.js のノードの形式に変換*/),
edges: res.result!.edges.map(/* G6.js のエッジの形式に変換*/),
};
graph.current!.data(data);
graph.current!.render();
});
return () => {
graph.current!.destroy();
graph.current = null;
}
}, []);
return <div ref={ref}></div>;
}
起動
以上作ったものをローカルで起動させてみました。
まず、DBは公式ドキュメントに従うとDockerコマンド一発で立ち上がります。
$ docker run -p7474:7474 -p7687:7687 -e NEO4J_AUTH=neo4j/s3cr3t neo4j
backend と Frontend はそれぞれ、gradle bootRun, yarn start として起動しました。
起動してみるとこんな感じです。簡素な画面ではありますが、数式のグラフを可視化できています。
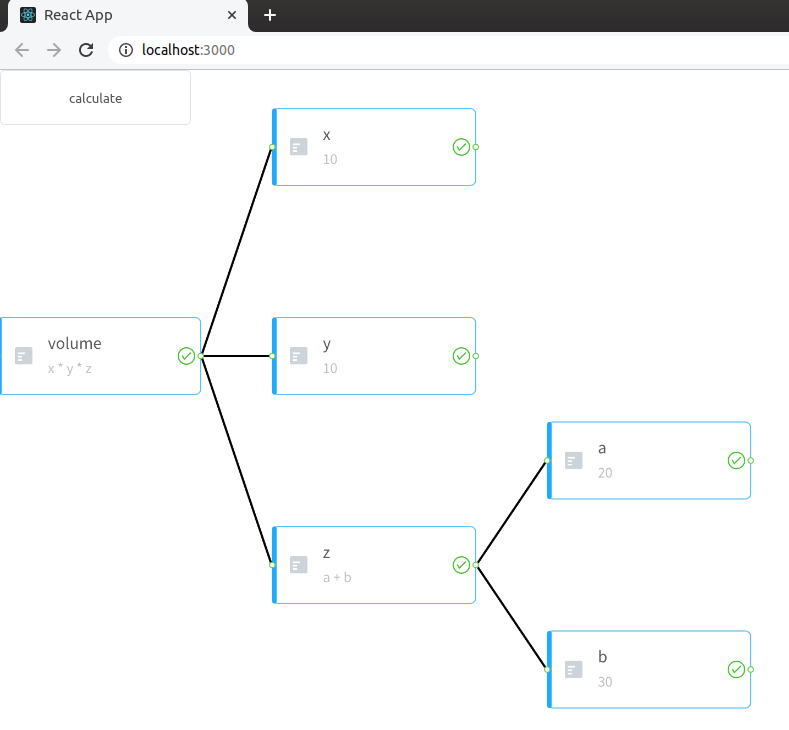
上のコードでは省略していますが、G6.jsのプラグインで、画面左上に計算処理を叩くボタンを用意して、押すと計算結果を alertするようにしてみました。
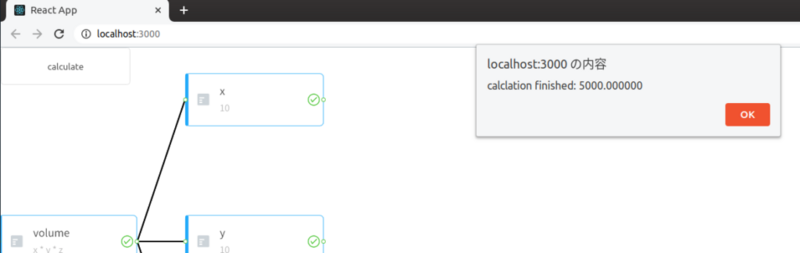
volume = 10 * 10 * (20 + 30) = 5000 なので、確かにちゃんと計算できています。
これで一応、数式グラフの保存・ロード・表示まではできたことになります。 今後はもう少し作り込んで、あわよくば仕事につながったら面白そうに思っています。
おわりに
今回は、コストモデルの背景や課題に加え、それをReactとNeo4jを用いて可視化する試みをご紹介しました。
私は元々CADアルゴリズムグループとして採用されたので、Webエンジニアは初めてまだ1年程です。しかし、この記事のような小さなシステムを自分で一から一通り作ってみると、中々いい勉強になりました。
また、ここに書いた実装は私1人では達成し得なかったことで、色々な方のアドバイスを経ながらできたものです。弊社にはこのように一緒に技術を楽しんでくれるメンバーが揃っておりますので、興味を持っていただいた方は、ぜひご連絡いただければと思います。