陰関数による形状表現 (1)

半径 $r$ の円の式を考えましょう。パラメトリック表現はこうです。

\left(\begin{array}{c}x(t) \\ y(t) \end{array}\right) = r\left(\begin{array}{c} \cos(t) \\ \sin(t) \end{array}\right)

対して、陰関数表現はこうです。

f(x, y) = \sqrt{x^2 + y^2} - r = 0

大体分かりましたね？大丈夫です、私も大体しか分かっていません。

関数 $f(x, y)$ に注目していきましょう。これは「原点を中心とし半径 $r$ の円からの符号付き距離」を表す関数です。

$(x, y)$ に円周上の点を入れると $f(x, y) = 0$、つまり円からの距離はゼロです。
$(x, y)$ に円の外側の点を入れると $f(x, y) > 0$ で、$f(x, y)$ は円からの（正の）距離です。
$(x, y)$ に円の内側の点を入れると $f(x, y) < 0$ で、$f(x, y)$ は円からの負の距離です。

はい、これで完全に理解()しました。$f(x, y)$ は円の外側は正、円の内側は負、絶対値は円までの距離を返す関数です。これを「符号付き距離（signed distance）」と言います。

$f(x, y) = 0$ が円周を表しているとも考えられるし、$f(x, y) \le 0$ が（中身の詰まった）円領域を表しているとも考えられます。ここでは後者の捉え方が重要です。円領域を集合の記法で書き表してみましょう。

A = \{ (x, y)\in R^2 \mid f(x, y) \le 0 \}

円領域が集合の記法で書けました。素晴らしいですね。

しかしこの表記だと、領域 $A$ が関数 $f$ から導出されるという雰囲気が伝わってきません。ちょっと改良して次のように書くことにしましょう。

D(f) = \{ (x, y)\in R^2 \mid f(x, y) \le 0 \}

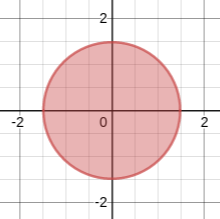
ここでは円を例に取っていますが、この形状表現は円に限定されません。関数 $f: R² \rightarrow R$ を $D$ に渡すことにより様々な図形（領域）を定義することができます。

さて、集合の記法で書くと、集合演算をしたくなりますね？

というわけで、もうひとつ別の円領域を作って集合演算をしてみます。中心座標 $(c_x, c_y)$、半径 $\tilde{r}$ の円領域を作ることとし、次の陰関数を定義します。

g(x,y) = \sqrt{(x-c_x)^2 + (y-c_y)^2} - \tilde{r}

すると新しい円領域は $D(g)$ と表記できます。では2つの円領域 $D(f)$ と $D(g)$ の集合演算を考えましょう。

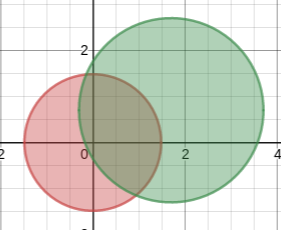
2つの円が重なっている領域は次式となります。

D(f)\cap D(g) = \{(x, y) \mid \max(f(x,y), g(x, y)) \le 0 \} = D(\max(f, g)) \\

2つの円領域を合わせた領域は次式となります。

D(f)\cup D(g) = \{(x, y) \mid \min(f(x,y), g(x, y)) \le 0 \} = D(\min(f, g)) \\

ただし、$\max(f, g)$、$\min(f, g)$ は次式で定義されるものとしています。

\max(f, g)(x, y) = \max(f(x, y), g(x, y)) \\ \min(f, g)(x, y) = \min(f(x, y), g(x, y))

非常に簡単に集合演算が表現できました。ここでは円領域を例に図示していますが、円以外の形状でも集合演算は同様に定義できます。パラメトリック表現ではこうはいきません。同じ演算をパラメトリック表現された2つの円で計算することを少し想像してみてください。2つの円の交点計算をし、交点が2つある場合と接する場合と交わらない場合に場合分けをし、…あーめんどくさい！

もう分かりましたね。陰関数による形状表現の利点はズバリ、

「集合演算がめちゃ簡単！」

です。

実はもうひとつ利点があるので、次回はそれを説明することにしましょう。こっちのほうが重要かもしれません。とっても簡単でほとんど自明なことなのですが、もったいぶって次に回すことにします。

欠点はないのでしょうか。もちろんあります。光あるところには必ず陰があるのです、陰関数だけに（あ、今読者が減りました）。それについても追々説明することにしましょう。

さしあたって簡単のために2Dの図形で説明していますが、そのうち3Dにも拡張していきましょう。

（つづく）